劣モジュラ関数を最小化する奇数サイズ集合

1. はじめに

今回は，奇数サイズの部分集合の中で，劣モジュラ関数値が最小なものを求める方法を紹介します．劣モジュラ関数が多項式時間で最小化できることは広く知られていますが，実は劣モジュラ関数を最小化する奇数サイズ集合も，通常の劣モジュラ最小化を繰り返し行うことで求めることができます．

2. アルゴリズム

$S$を有限集合，$f:2^S\rightarrow \mathbf{R}$を劣モジュラ関数とします．ここで，$f$が劣モジュラであるとは，すべての部分集合$X,Y\subseteq S$に対して劣モジュラ不等式$f(X)+f(Y)\geq f(X\cup Y)+f(X\cap Y)$が成り立つことをいいます．$f(X)$の値が最小となる奇数サイズの$X\subseteq S$を求めるアルゴリズム [1,2]*1*2を以下で説明します．紹介するアルゴリズムは，部分集合$T\subseteq S$に対して，$|X\cap T|$が奇数サイズとなる$X\subseteq S$の中で$f$を最小化するものを求めるという少し一般化された設定のものです*3*4．

まず，$|T|$が奇数のときは，以下のように$|T|$が偶数の場合に帰着します：各$t\in T$に対して，$S\setminus \{t\}$の部分集合であって$T\setminus \{t\}$との交叉が奇数サイズのもののうち$f$を最小化する集合を求め，それらについての$f$の値と$\min\{f(U)\mid U\supseteq T\}$を比べ，最小のものを出力すればokです．以下では$|T|$が偶数の場合を考えます．

まず，通常の劣モジュラ最小化アルゴリズムで，$X\cap T,T\setminus X\neq \emptyset$を満たす$X\subseteq S$（このような$X$を$T$を分割する集合とよぶことにします）のうち$f(X)$を最小化するものを求めます．これは，各$s,t\in T$に対して$s$を含み$t$を含まない集合の中で$f$を最小化するものを求めることで達成できます．$|X\cap T|$が奇数ならokです．$|X\cap T|$が偶数のときは，$Y\subseteq S$であって，$T\setminus X$を分割せず，かつ$|X\cap T\cap Y|$が奇数なものの中で$f$を最小化するものと，$Z\subseteq S$であって，$X\cap T$を分割せず，かつ$|(T\setminus X)\cap Z|$が奇数なものの中で$f$を最小化するものを求めます（これは，$T\setminus X$や$X\cap T$を縮約して一要素にし，$T$のサイズがより小さい場合のアルゴリズムを回すことで帰納的に求められます）．そして，$Y$と$Z$のうち$f$の値が小さいものを出力すると，実はそれが$T$との交叉が奇数サイズの集合の中で$f$の値を最小化するものになっています！以下でその証明をします．

矛盾を導くために，$|W\cap T|$が奇数の集合$W\subseteq S$の中で$f(W)$を最小化するものが，$f(W)<f(Y),f(Z)$を満たすと仮定します．$|W\cap X\cap T|$と$|W\cap (T\setminus X)|$のどちらか一方は奇数なので，$|W\cap X\cap T|$が奇数の場合を考えます（$|W\cap (T\setminus X)|$が奇数の場合も同じ流れで示せます）．すると$f(W)<f(Y)$と$Y$の最小性から，$W$は$T\setminus X$を分割することが分かります．つまり$W\cup X$は$T$を分割するので，$X$の最小性から$f(X)\leq f(W\cup X)$が成り立ちます．また，$|W\cap X\cap T|$は奇数なので，$W$の最小性から$f(W)\leq f(W\cap X)$が成り立ちます．これと劣モジュラ不等式$f(W)+f(X)\geq f(W\cup X)+f(W\cap X)$から，$f(W)=f(W\cap X)$が成り立ちます．$W\cap X$は$T\setminus X$を分割しないので，$Y$の最小性から$f(Y)\leq f(W\cap X)=f(W)$が成り立ちますが，これは仮定に矛盾します．

計算量については，$|T|$が偶数の場合は帰納法のステップが$O(|T|)$回あり，各ステップで劣モジュラ最小化問題を$O(|T|^2)$回解くことになるので，合計$O(|T|^3)$回劣モ最小化をする必要があります．

3. コメント

やや複雑ですが，なんだかパズル的で面白い話ですね．

また，この結果はparity family上の劣モジュラ関数最小化問題に拡張されています [3]．$\mathcal{F}\subseteq 2^S$がparity familyであるとは，すべての$X,Y\in 2^S\setminus \mathcal{F}$に対して，$X\cup Y,X\cap Y$が両方とも$\mathcal{F}$に属するか，両方とも属さないかのどちらかが成り立つことをいいます．parity familyは奇数サイズ集合の全体からなる族の一般化ですが，parity familyに属する集合の中で劣モジュラ関数値が最小のものを求める問題も，通常の劣モジュラ最小化を繰り返し行うことで多項式時間で解くことができます．

参考文献

[1] M. Grötschel, L. Lovász, and A. Schrijver. The ellipsoid method and its consequences in combinatorial optimization. Combinatorica, 1:169–197, 1981.

[2] M. Grötschel, L. Lovász, and A. Schrijver. Corrigendum to our paper ``The ellipsoid method and its consequences in combinatorial optimization''. Combinatorica, 4:291–295, 1984.

[3] M. X. Goemans and V. S. Ramakrishnan. Minimizing submodular functions over families of sets. Combinatorica, 15:499–513, 1995

*1:もととなるアルゴリズムは[1]で発表されましたが，そこには間違いが含まれていて[2]で修正されました．自分も最初は[1]のアルゴリズムが正しく動くと思ってここに書いてしまっていました．．

*2:実は[1]は劣モジュラ最小化問題に対する初の（弱）多項式時間アルゴリズムを与えた論文でもあります．

*3:こちらのほうが計算量などのパートが説明しやすいので

*4:このアルゴリズムはSchrijver ABCにも載っているので，気になる方は参照すると良いです．

マトロイドに対する貪欲法でないアルゴリズム

今回は，マトロイドの最大重み基を求める貪欲法でないアルゴリズムを紹介します*1．

マトロイドの最大重み基は，重みの大きな要素から選んでいく貪欲法によって求められます．この事実は多分有名だと思いますが，ではそれ以外の方法でマトロイドの最大重み基を求めることはできるのでしょうか？

実は，貪欲法よりももう少しテキトーな順番で要素を選んでいっても，最大重み基を求めることができます．今回はその方法を紹介します*2．

1. 定義など

マトロイドの用語の定義をします．知っている方は飛ばしてもらって大丈夫です．

 $E$を有限集合とする．$\mathcal{I}\subseteq 2^E$に対して，$M:=(E,\mathcal{I})$がマトロイドであるとは，次の三つの条件を満たすことをいう．

1. $\emptyset \in \mathcal{I}$,
2. $X\subseteq Y\in \mathcal{I}\Rightarrow X\in \mathcal{I}$,
3. $X,Y\in \mathcal{I},\ |X|<|Y|\Rightarrow \exists e\in Y\setminus X\ $s.t. $X+e\in \mathcal{I}$.

$E$を$M $の台集合とよび，$\mathcal{I}$に属する集合を独立集合とよぶ．$\mathcal{I}$を独立集合族とよぶ．また，極大な独立集合を基とよび，基をすべて集めてできる集合族を基族とよぶ．マトロイドのすべての基のサイズは等しいことが知られている．

マトロイド$M=(E,\mathcal{I})$の基族を$\mathcal{B}$とおく．$M $の双対マトロイド$M^*$とは，台集合が$E$であり，次のように定義される基族$\mathcal{B}^*$をもつマトロイドである．

$$\mathcal{B}^*:=\{B\subseteq E\mid E\setminus B\in \mathcal{B}\}.$$

 つまり，$\mathcal{B}^*$は$\mathcal{B}$に属する基の補集合を集めた集合族である． $M^*$の独立集合族は$\mathcal{B}^*$に属する基の部分集合たちからなる族，つまり$\mathcal{I}^*:=\{X\subseteq E\mid \exists B\in \mathcal{B}^* \mathrm{s.t.} X\subseteq B\}$である．

マトロイド$M=(E,\mathcal{I})$に対して，独立集合でない集合$X\notin \mathcal{I}$を従属集合とよぶ．極小な従属集合をサーキットとよぶ．また，双対マトロイド$M^*$のサーキットをコサーキットとよぶ．

2. 問題設定とアルゴリズム

以下のマトロイドの最大重み基問題を考えます．

マトロイドの最大重み基問題

入力: マトロイド$M=(E,\mathcal{I})$*3，重み関数$w:E\rightarrow \mathbf{R}$

タスク: $\sum_{b\in B} w(b)$が最大の基$B $を求める．

 この問題に対するアルゴリズムとして，空集合$F:=\emptyset $から始めて，重みの大きい順に要素を選んでいき，その要素を$F $に加えても独立集合のままなら順次$F$に加えていく，という貪欲アルゴリズムは有名だと思います．実は，このアルゴリズムよりも少しテキトーな順番で要素を選んでいく次のようなアルゴリズムでも，きちんと最大重み基を求めることができます．

アルゴリズム

• $F:=\emptyset$.
• $M $のコサーキットであって，$F$と交わらないもの$C^*\subseteq E\setminus F$があれば，どれでも良いので一つ選ぶ．この$C^*$に含まれる要素の中で最大重みのものを$F$に加える．これを繰り返す．
• そのようなコサーキットがなければ，$F$を出力する．実はこの$F$が最大重みの基になっている．

このアルゴリズムは，$M $の任意の基$B$がコサーキット$C^*$と必ず交わるので，とりあえず$C^*$に含まれる要素の中で最大重みのものを基の要素として採用していく，ということをしています．これもある意味貪欲法と呼べるかもしれません．重みが大きい順に要素を選んでいく貪欲法も上のアルゴリズムの特殊ケースとして見ることができて，$E\setminus F$における最大重みの要素を含むコサーキットが（あれば）常に選ばれる場合に対応します*4．

それではこのアルゴリズムの正当性を示していきます．

アルゴリズムの正当性

次の二つを順に示す．

1. $F$が常に$M $の独立集合であること
2. 最終的に出力される$F$が$M $の最大重み基であること

1.の証明

 まず重要な補題を一つ示す:

補題

マトロイド$M $の任意のサーキット$C$とコサーキット$C^*$に対して，$\left|C\cap C^*\right|\neq 1.$

証明

$C\cap C^*=\{e\}$と仮定する．すると，$C-e,\ C^*-e$はそれぞれ$M,\ M^*$の独立集合である．さらに，仮定から$C-e,\ C^*-e$は交叉しない．$C^*-e$は$M^*$の独立集合なので，$C^*-e$を含む$M^*$の基が存在し，その補集合は$C^*-e$を含まない$M $の基である（$B$とおく）．$B$と$C-e$に対して，マトロイドの定義の条件3を繰り返し用いることで，$C-e$を含み，$C^*-e$を含まない$M $の基$B'$が得られる．すると$E\setminus B'$は$M^*$の基であり，$C^*-e$を含む．$B'$と$E\setminus B'$のどちらかは$e$を含むが，これは両者の独立性に矛盾． $\Box$

1.の証明に入る．アルゴリズムの始めの時点では，$F$は空集合なので独立集合である．アルゴリズムのある段階で，コサーキット$C^*\subseteq E\setminus F$の最大重みの要素$e$が選ばれ，$F\in \mathcal{I}$かつ$F+e\notin \mathcal{I}$であったとする．このとき，$F+e$は従属集合なので，$e$を含むサーキット$C\subseteq F+e$が存在する．ここで，コサーキット$C^*$とサーキット$C$は$e$を含むので，補題から$\left|C\cap C^*\right|\geq 2$がわかる．しかし，$C^*\subseteq E\setminus F,\ C\subseteq F+e$なので，$\left|C\cap C^*\right|\leq 1$であり矛盾． $\Box$

2.の証明

まず，最終的に出力される$F$が$M $の基であることを示す．$E\setminus F$に包含されるコサーキットが存在しない場合，$E\setminus F$は$M^*$の独立集合である．さらに，1.から，最終的に出力される$F$は$M $の独立集合なので，この$F$は$M $の基である．

次に，アルゴリズムのどの段階でも，$F$を包含する$M $の最大重み基が存在することを示す．これを示せば，最終的に出力される$F$が$M $の最大重み基であることがわかる．アルゴリズムの始めの時点では，$F$は空集合なので$F$を包含する最大重み基は存在する．アルゴリズムのある段階で，$F$を包含する最大重み基が存在し，次に$F$に加える要素としてコサーキット$C^*\subseteq E\setminus F$の最大重みの要素$e$が選ばれたとする．$F$を包含する最大重み基を$B$とおく．$B+e$の部分集合であるサーキット$C\subseteq B+e$に対して，$C$は$e$を含むので，補題から$\left|C\cap C^*\right|\geq 2$がわかる．$e$と異なる$e'\in C\cap C^*$をとると，$e$の選び方から$w(e')\leq w(e)$が成り立つ．ここで，$B+e-e'$は，$M $の基であり*5，重みは$B$の重み以上である．さらに，$F+e\subseteq B+e-e'$なので，$B+e-e'$は$F+e$を包含する$M $の最大重み基である． $\Box$

これでアルゴリズムの正当性を示すことができました．

 余談

最小全域木問題は，マトロイドの最大（小）重み基を求める問題の特殊ケースとして見ることができます．最小全域木問題には，マトロイドの貪欲法に対応するKruskal法と呼ばれるアルゴリズムが知られています．一方で，Primのアルゴリズムと呼ばれる，連結性を保つという条件のもと最小重みの辺を順次加えていくアルゴリズムでも最小全域木問題を解くことができます．では，マトロイドに対してもPrimのアルゴリズムに対応するものは考えられるのでしょうか？

実は，2章で紹介したアルゴリズムは，Primのアルゴリズムも特殊ケースとして（ある意味）含んでいます．つまり，Primのアルゴリズムは，すでに選ばれた辺によって連結になっているグラフの頂点たちと，それ以外の頂点をカットする辺の集合の中から，最も重みの小さな辺を選んでいくアルゴリズムです．グラフ的マトロイドのコサーキットは元のグラフの極小カットなので，Primのアルゴリズムは，カットの中で最小重みの辺を含む（カットの部分集合である）極小カットが常にコサーキットとして選ばれる場合の2章のアルゴリズム，と理解することができます（ちょっと強引かもしれませんが）．

*1:ブログ名が「blogoid」でありながら，実はマトロイドの記事を書くのは初めてです．

*2:元ネタは，コルテフィーゲンの「組合せ最適化」の演習問題（6章の問題8）で，今回はそれのマトロイド版です．

*3:細かいことを言うと独立性オラクル（$X\in \mathcal{I}$かどうかを定数時間で判定してくれるオラクル）で与えられる設定を考えます．

*4:$M $の独立集合$F\in \mathcal{I}$と要素$e\in E\setminus F$に対して，$F+e\in \mathcal{I}$であることと，$e$を含む$M $のコサーキット$C^*\subseteq E\setminus F$が存在することは同値なので．

*5:マトロイドの独立集合$I$に要素$e$を加えて従属集合になったとき，$I+e$が部分集合として持つサーキットは唯一つという性質を暗に用いています．

今まで読んだ数学の本

久々の更新ですが，今回は今まで読んだ数学の本を紹介します*1*2．離散数学や組合せ最適化の本がメインです．

  グラフ理論 （R. Diestel） 

グラフ理論 (Springer‐Verlag GTMシリーズ)

 グラフ理論について広く浅く書かれている本．日本語で書かれたグラフ理論の本では多分一番詳しい．特徴としてはグラフマイナーについての章があるのが珍しいという感じ（グラフマイナー定理の証明も概略は載っている）．

離散凸解析と最適化アルゴリズム（室田一雄，塩浦昭義） 

離散凸解析と最適化アルゴリズム (数理工学ライブラリー)

 離散凸解析の本．離散凸解析と組合せ最適化問題やアルゴリズムのつながりに重点をおいて説明している．構成としては，前半でいくつか組合せ最適化問題を紹介し，後半で離散凸解析を導入しがてら紹介した組合せ最適化問題との関連を述べている．離散凸解析自体の説明は後半でしか出てこないためちょっと少なめ．

グラフ・ネットワーク・マトロイド（伊理正夫，藤重悟，大山達雄）

グラフ・ネットワーク・マトロイド (講座・数理計画法)

かなり昔の本（1986年発売）だけど，マトロイドの話が載っている数少ない日本語書籍．1986年当時の最先端のグラフ・ネットワーク・マトロイドの話が書いてあるが，今見るとトピックの選び方がマニアックに見えたりして面白い．計数工学科の基礎数理っぽさを感じる内容の本．今は絶版で中古でしか入手できない．

量子コンピュータ入門（宮野健次郎，古澤明）

量子コンピュータ入門(第2版)

量子回路や量子アルゴリズムについて載っている本．特に素因数分解の量子アルゴリズムとして有名なShorのアルゴリズムが丁寧に紹介されている．量子力学の知識がない人でも内容がわかるように書かれているので，手っ取り早く量子アルゴリズムに入門したい人におすすめ．

 計算理論の基礎 (M. Sipser)

計算理論の基礎 [原著第2版] 1.オートマトンと言語

計算理論の基礎

 1,2,3巻がある．下のものは分冊になる前の古い版で，自分はこちらを読んだ*3．オートマトン，形式言語，計算可能性，計算量など計算理論分野の話題が幅広く載っている．定理の証明などで，直感的な説明をしたあとに厳密な証明を書くというスタイルを取っており，非常に読みやすくわかりやすい．

組合せ最適化 (B. Korte, J. Vygen)

組合せ最適化 第2版 (理論とアルゴリズム)

組合せ最適化の幅広いトピックの基礎が網羅されている本．組合せ最適化の勉強をするときは一家に一台あると便利かもしれない．行間少なめ．説明はわかりやすさ重視というよりは文字数が最小になるような説明方法が選択されている感じがして，ページ数あたりの情報量が多い．

 Combinatorial Optimization (A. Schrijver)

Combinatorial Optimization (Algorithms and Combinatorics (24))

 A,B,Cの3分冊になっている組合せ最適化の教科書（英語）．通称Schrijver ABC．合計1800ページ超えで，Cは半分以上がreferenceに費やされている．内容としては2000年代前半までの組合せ最適化の話題の大部分を網羅しているという感じで，研究のサーベイにも使えるレベルで詳しい*4．組合せ最適化の研究で何かサーベイするときはとりあえずこれを読んでみるのもありかもしれない．

*1:本当は数学のちゃんとした記事も書きたいのですが，エネルギーを使うのと，研究を始めたせいで気持ち的に下手なことを書けなくなった（？）ために最近書けてないです．

*2:読んだと言っていますが，実はまだ読みかけの本も多いです．積読消化していきたいです．

*3:古本屋で安く売っていたので

*4:自分は組合せ最適化のあるトピックについて頑張ってネットでサーベイしたあとでSchrijver ABCを読んだところ，サーベイした内容がほぼすべて載っていたことがあります．

分離問題とLP

線形計画問題が楕円体法などによって多項式時間で解けることは有名です．しかし，例えばある問題のLP表現において，制約式の個数がその問題の入力長に関して指数個あった場合，その問題は普通の楕円体法では多項式時間で解くことはできません．では，そのようなLPが（元の問題の入力長に関する）多項式時間で解ける場合はあるのでしょうか？

実は，分離問題と呼ばれる問題が多項式時間で解けるなら，LPは制約式の個数にはよらない多項式時間で解くことができます．多面体$P$（多面体とは，$\mathbb{R}^n$におけるいくつかの線形不等式によってつくられる領域のことです．例えば，LPの実行可能領域は多面体です）に対する分離問題とは次のような問題です:

分離問題

    入力: ベクトル $y\in \mathbb{R}^n$

タスク: $y\in P$かどうかを判定し，$y\notin P$なら$c\in \mathbb{R}^n$であって$c^Ty>\mathrm{max} \{c^Tx\mid x\in P\}$を満たすものを返す．

$y\notin P$のときに返す$c$は$P$と$y$を分離する超平面の傾きになっています．

 あるLPの実行可能領域を多面体$P$とします．$P$に対する分離問題の多項式時間オラクル*1が存在し，かつ$P$をつくる線形不等式たちのビット長の上界がわかっているなら，そのLPは制約式の個数によらない多項式時間で解けるという非常に強い定理が成り立ちます．

定理 [1]

 多面体$P$に対する分離問題の多項式時間オラクルが存在し，かつ$P$を表現するある有理数係数の線形不等式系に対して，各不等式のビット長が$\varphi$で抑えられるような$\varphi$が得られているとする．このとき，実行可能領域が$P$であるLPは，その目的関数の係数$c$のビット長と$\varphi$に関する多項式時間で解くことができる．

ちなみに，多項式時間で解けるの内訳として，分離問題のオラクルの呼び出しと初等的操作の回数は$\varphi$に関する多項式で抑えられ，途中で出てくる数のビット長は$\varphi$と$c$に関する多項式で抑えられます．

 参考文献

 [1] M. Grotschel, L. Lovasz, A. Schrijver, Geometric Algorithms and Combinatrial Optimization, Springer, Heidelberg, 1988.

*1:ここでは多項式時間オラクルの定義として，入力に対して多項式時間で正しい解を多項式長のビット列として返すというものを考えます．計算複雑性理論などで用いられる厳密なオラクルの定義についてはComputational Complexity(S. Arora, B. Barak)などを参照すると良いです(教えてくださったNさんありがとうございます).

数理情報学専攻予想問題

院試勉強にもそろそろ飽きてきたので、気分転換に数理情報学専攻の専門数学の予想問題を作ってみました。計数工学科内では有名な（？）話題に関する問題ですが、ちょっとマニアックなので、暇な人は解いてみてください。難易度は難しめ（&分量多め）だと思います。

問題

 無向グラフ$G=(V, E)$を、2つの頂点集合$R, C\subseteq V$（$R\cap C=\emptyset, R\cup C=V$）と、辺集合$E\subseteq \{(r, c)\mid r\in R, c\in C \}$をもつ2部グラフとする。この2部グラフ$G$に対して、DM分解（Dulmage-Mendelsohn分解）と呼ばれる頂点集合$V$の分割を考える。まず、DM分解は次のようなアルゴリズムによって得られる:

DM分解アルゴリズム

1. $G$の最大マッチング$M $を1つ見つけ、$M $の端点の集合を$\partial M $とする。
2. $G$において、$E\setminus M $の辺を$R$から$C$へ向かうように向き付けした有向辺と、$M $の辺を$R$から$C$、$C$から$R$へ向かうようにそれぞれ向き付けした有向辺からなる集合を$\tilde{E}$とする。$\tilde{G}=(V, \tilde{E})$とする。
3. $\tilde{G}$において、$R\setminus \partial M $の頂点から有向辺をたどって到達できる頂点全体の集合（$R\setminus \partial M $の頂点も含む）を$V_{\infty}$とし、$C\setminus \partial M $の頂点に有向辺をたどって到達できる頂点全体の集合を$V_{0}$とする。
4. $\tilde{G}$から$V_0\cup V_{\infty}$の頂点（とそれに接続する辺）を除去したグラフの強連結成分分解$\{V_k \mid 1\leq k \leq p\}(\emptyset \neq V_k \subseteq V)$を求める。ただし、$V_1, V_2, ..., V_p$は強連結成分であり、$l<k$のとき$V_k$から$V_l$への有向道がないように番号づける。

ここで得られた$V$の分割$\{V_k \mid k=0, 1, ...,p, \infty \}$のことを$G$のDM分解と呼ぶ。

(1)  次の図1の2部グラフ$H$のDM分解（頂点集合の分割）を求めよ。

以下、$G$のDM分解$\{V_k \mid k=0, 1, ...,p, \infty \}$について考える。

(2)  頂点集合$(R\setminus V_{\infty})\cup (C\cap V_{\infty})$が$G$の最小頂点被覆であることを示せ。

(3)  頂点集合$V$において、頂点$s, t$を新たに追加し、$V'=V\cup \{s, t\}$とする。また、頂点$s$から$R$の各頂点へのコスト1の有向辺と、$C$の各頂点から$t$へのコスト1の有向辺、および$E$の各辺を$R$から$C$へ向かうように向き付けしたコスト2の有向辺からなる辺の集合を$E'$とする。$G'=(V', E')$とする。このとき、カット$(\{s\}\cup V_{\infty}, \ V'\setminus (\{s\}\cup V_{\infty}))$が$G'$の最小$s$-$t$カットであることを示せ。ただし、$G'$の最小$s$-$t$カットとは、頂点$s$と$t$を分離するカットのうち、コストが最小のカットのことである。

(4)  $\{V_k \mid k=0,1,...,p, \infty\}$に対して次のように半順序を定める:

$V_k \preceq V_l \Longleftrightarrow k=\infty$または$l=0$または$\tilde{G}$において$V_l$の頂点から$V_k$の頂点への有向道が存在する

この半順序から定まるイデアル全体の族を$I$とする。つまり、

$I=\{A \mid A\subseteq \{V_k \mid k=0,...,p,\infty\},V_l \in A$かつ$V_k \preceq V_l $なら$V_k\in A \}$

このとき、$\forall A\in I(A\neq \emptyset, \{V_k \mid k=0,...,p,\infty\})$について、$S_A=\{v \mid v=s$ または$\exists V_k\in A,\ v\in V_k\}$とすると、カット$(S_A,V'\setminus S_A)$が$G'$の最小$s$-$t$カットであることを示せ。

(5)  逆に、$G'$の任意の最小$s$-$t$カットはある$A\in I$を用いて$(S_A,V'\setminus S_A)$と表せることを示せ。

解答↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓

解答（略解）

(1)  

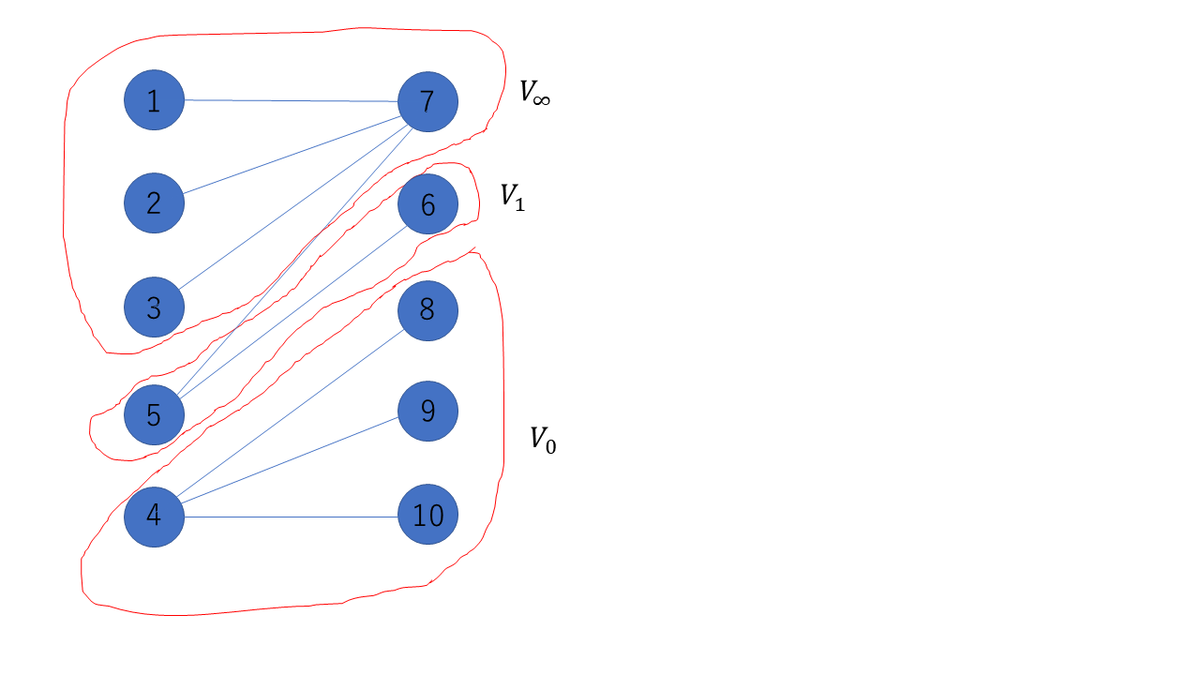
(2)  $(R\setminus V_{\infty})\cup (C\cap V_{\infty})$が$G$の頂点被覆であることは構成からわかる。最小性は、被覆に必要な頂点数は最大マッチングの本数で下から抑えられるが、$(R\setminus V_{\infty})\cup (C\cap V_{\infty})$の頂点数は最大マッチング$M $の本数に等しいのでOK。

(3)  最大マッチング$M $の各辺$(r,c)(r\in R,\ c\in C)$について、$s\rightarrow r\rightarrow c\rightarrow t$という有向道に着目する。

すると、この有向道の辺$(s, r), (r, c), (c, t)$のうち少なくとも1本は$s$と$t$を分離するカットに含まれることがわかる。ゆえに、最小$s$-$t$カットのコストは最大マッチング$M $の本数で下から抑えられるが、カット$(\{s\}\cup V_{\infty}, \ V'\setminus (\{s\}\cup V_{\infty}))$のコストは最大マッチング$M $の本数に等しいので、このカットは最小$s$-$t$カットである。

(4)  カット$(S_A,V'\setminus S_A)$のコストは(3)の最小$s$-$t$カットとのコストと同じなので、$(S_A,V'\setminus S_A)$も最小$s$-$t$カット。

(5)  $G'$において$s$から最大流を流して（コストを辺容量とみる、最大流は最大マッチング$M $に流れるようにする）残余グラフをとる。このとき残余グラフ上で容量をコストとみたときのコスト0の$s$-$t$カット全体は(4)で出てきたカット$(S_A, V'\setminus S_A)$全体に等しい。また、この残余グラフ上のコスト0の$s$-$t$カット全体は$G'$の最小$s$-$t$カット全体に等しい。よって、$G'$の$s$-$t$最小カット全体は、(4)で出てきたカット$(S_A,V'\setminus S_A)$全体に等しい（(3)と(4)も実はこれで示せます）。

解説

ここで問題の背景について少し解説します。

任意のグラフに対して最大流を流して残余グラフを構成し、そのグラフ上で始点（ソース）からたどりつける頂点全体の集合、終点（シンク）にたどりつける頂点全体の集合、それらを残余グラフから除いて強連結成分分解して得られた強連結成分をそれぞれとります。これに対して互いの頂点集合を行き来できるかという半順序を定義し、その半順序から定まるイデアル族をとると、実はこれが最小カット全体の集合になっている、という事実が成り立ちます。これの2部グラフでの特殊な場合がDM分解となるわけです。

雑感

改めて問題を作ってみると、DM分解は意外と定義など説明すべきことが多いので、院試には出しにくいのではないかという気持ちになってきました。でもDM分解は計数工学科一押しのトピックなので、いつか院試に出てくれたら嬉しいですね。

すべての頂点の次数が3以上のグラフは$K_4$をマイナーとして含む話

今回は、すべての頂点の次数が3以上のグラフは$K_4$をマイナーとして含むという話を紹介しようと思います。一見簡単そうな主張ですが、厳密に証明するのは意外と大変です。

1. 主張の内容

以下の主張が成り立ちます。

 $G=(V, E)$を無向単純グラフ*1とする。このとき、$G$のすべての頂点$v\in V$の次数が3以上であれば、$G$は$K_4$をマイナー*2として含む。

2. 証明

まず、グラフ$G$が非連結であれば連結成分ごとに考えればよいので、以下では$G$が連結である場合を考える。

$G$の頂点数に関する帰納法で示す。

$G$から適当に頂点$v\in V$を選ぶ。$v$の次数は3以上なので、$v$と隣接する頂点$u$が存在する。このとき、$v, u$の両方と隣接する頂点が存在しないなら、辺$(v, u)$を縮約すれば、すべての頂点の次数が3以上で頂点数が$|V|-1$の単純グラフになるので帰納法がまわる。ゆえに$v, u$の両方と隣接する頂点$w$が存在する場合を考える。

 このとき、$u, v, w$を縮約して1つの頂点にしたときに多重辺ができないのであれば、そのように縮約すれば先ほどと同様に帰納法がまわる。よって、以下では$u, v, w$を縮約して1つの頂点にしたときに多重辺ができる場合、つまり$u, v, w$のうちの少なくとも2頂点と隣接する頂点$x$が存在する場合を考える（どの頂点と隣接しても同じなので、$x$は$u, w$に隣接するとする）。

このとき、$v$と$x$を結ぶ辺がある場合は$K_4$をマイナーとして含むのでOK。そうでない場合を考えると、頂点$u, v, w, x$から$V\setminus \{u, v, w, x\}$へ伸びている辺は2本である場合と3本以上である場合がある。

2本である場合を考える。この場合2本の辺は$v, x$から伸びている辺である。$v, x$と隣接している頂点をそれぞれ$a, b$とする。

 ここで、$G$から$u, v, w, x$を取り除いたときに$a, b$が同じ連結成分に含まれるなら、縮約することで$v, x$の間に辺をつくることができるので$K_4$をマイナーとして含みOK。ゆえに$u, v, w, x$を取り除いた時に$a, b$が異なる連結成分に含まれる場合を考えればよいが、この場合も$v, u, w, x$を取り除き、$a$と$b$を辺でつなげば帰納法がまわる。

  次に頂点$u, v, w, x$から$V\setminus \{u, v, w, x\}$へ伸びている辺が3本以上である場合を考える。このとき、$u, v, w, x$を縮約して1つの頂点にしたときに多重辺ができないなら、そのように縮約すれば帰納法がまわるので、以下では多重辺ができる場合、つまり$u, v, w, x$のうちの少なくとも2頂点と隣接する頂点$y\in V\setminus \{u, v, w, x\}$が存在する場合を考える（$y$は$v, w$と隣接するとする。$v, x$と隣接するとすると、$K_4$をマイナーとして含むことに注意）。

この場合も先ほどと同様に考えることができる。まず、上図の部分グラフ$G'$は次の2条件を満たしていることに注意する。

1. 三角形をいくつか張り合わせたグラフになっている
2. 次数2の頂点が2つ以上存在する

 ここで、一般に条件1を満たすグラフの非隣接2頂点の間に1本辺を加えたグラフは、$K_4$を必ずマイナーに持つことに注意する*3。

$G'$に対して先ほどと同様に場合分けして考える。

まず条件2から、$G'$で次数2の2頂点を結ぶ辺が$G$にあるか、もしくは$u, v, w, x, y$から$V\setminus \{u, v, w, x, y\}$へ伸びている辺が2本以上あるかのどちらかが成り立つ。

まず$G'$で次数2の2頂点を結ぶ辺$e$が$G$にある場合、条件1から$G'$の非隣接2頂点の間に辺を加えると$K_4$をマイナーに持つので、$G'$に$e$を加えることで$K_4$をマイナーに持つグラフが得られてOK。

次に$u, v, w, x, y$から$V\setminus \{u, v, w, x, y\}$へ伸びている辺が2本以上ある場合を考える。2本なら、$G$から$u, v, w, x, y$を取り除くと$V\setminus \{u, v, w, x, y\}$の中で$x, y$に隣接していた2頂点は異なる連結成分に属する（これも先ほどと同じく条件1からわかる）ので、その2頂点を辺で結べば帰納法がまわる。3本以上なら、$u, v, w, x, y$を1頂点に縮約して多重辺ができないなら帰納法がまわり、多重辺ができるなら$u, v, w, x, y$のうち少なくとも2頂点と隣接する頂点$z\in V\setminus \{u, v, w, x, y\}$が存在する。ただし条件1から$z$が$G'$で互いに隣接しない2頂点に隣接するなら、$G$は$K_4$をマイナーに持つので、そうでない場合を考えればよい。つまり、$G'$に、頂点$z$と$z$から$u, v, w, x, y$のうちの2頂点に伸びる2辺を加えてできる$G$の部分グラフ$G''$も、三角形をいくつか張り合わせたグラフとなり、また$G''$には次数2の頂点が2つ以上存在する。よって$G''$は条件1、2を満たす。ゆえに$G''$に対しても同じ議論を繰り返していけば、帰納法がまわるか部分グラフの頂点が増えていくかのどちらかなので、$G$の頂点数が有限であることからいつかは帰納法がまわることになり、証明が完了する。

3. 余談1

話題に若干唐突感があると思うので、今回の主張を考えたくなった経緯を少し書いておきます。もともと「グラフ$G$の木幅*4が2以下⇔$G$は$K_4$をマイナーとして含まない」という主張を示したかったのですが、←側の証明をする際に、次数2以下の頂点があれば帰納法がうまく回るけど、すべての頂点の次数が3以上の時は帰納法が回らないので困っていました。そこで、$K_4$をマイナーとして含まないなら次数2以下の頂点が必ず存在すれば都合が良いなとなり、今回示した命題にたどり着きました。

4. 余談2

実は今回証明した主張よりももう少し強い主張が成り立ちます:

主張

 無向単純グラフ$G$のすべてのマイナーの最小次数が2以下であることと、$G$が$K_4$をマイナーとして含まないことは等価である。

 また、似たような主張として次のようなものも成り立ちます:

主張

無向単純グラフ$G$のすべてのマイナーの最小次数が3以下であることと、$G$が$K_5, K_{2, 2, 2}$をマイナーとして含まないことは等価である。

これらの主張も含め、グラフの最小次数と禁止マイナーについては

arxiv.org

に詳しく載っているので、興味のある方は参照してみてください。

*1:頂点数は有限とする。

*2:グラフ$G$に対して、辺の除去、頂点の除去、辺の縮約を繰り返して得られるグラフを$G$のマイナーと呼びます。

*3:この事実はここでは証明なしで認めることにします。証明はそこまで難しくはないはず。

*4:木幅については以前ブログで解説しています。

Cardinal Treeの数え上げ

最近輪講で"Compact Data Structures(Gonzalo Navarro, 2016)"という本を読んでいるのですが、そこでCardinal Treeと呼ばれる木の個数がn頂点のとき$$\frac{\binom{nk+1}{n}}{nk+1}$$個（$k$は子の最大個数）であると紹介されていました。その証明を考えてみたところなかなか面白かったので、紹介してみようと思います*1。

1. Cardinal Treeとは

子に1以上k以下のラベルが付いていて、同じ親を持つ子同士でラベルの重複がない（つまり1つの親が持てる子の最大個数はk個）根付き木のことをCardinal Treeといいます。

n頂点の順序木の個数がn-1に対するカタラン数であることは有名ですが、これは漸化式を用いて求める方法が一般的らしいです。同様にCardinal Treeの個数も漸化式で求めようとすると、これはなかなかうまくいきません。しかし、実はCardinal Treeの個数は、Cardinal Treeをビット列として表して、Cardinal Treeの条件を満たすようなビット列の個数を数え上げることでうまく求められるのです！これを次節で紹介します。

2. Cardinal Treeの数え上げ

さて、n頂点のCardinal Treeの個数を数え上げるための準備として、まずCardinal Treeをビット列として表してみます。

Cardinal Treeのビット列による表現は、Cardinal Treeの各頂点に長さkのビット列を対応させ、そのビット列が頂点が持つ子のラベルを表すというものです。

例えば、先ほど例に出したCardinal Treeのビット表現は

となります。

つまり、まず根に対応する長さkのビット列から始まり、次に根の子の数だけ根の子に対応する長さkのビット列が続き、次に根の孫のビット列が続き…というようなビット表現となります。

さて、このようにCardinal Treeをビット列で表したとき、頂点数をnとすると、長さがnkで、1がn-1個含まれるビット列になります。そこで、まずは安直に、長さnkで、1がn-1個含まれるビット列の個数を求めてみると$$\binom{nk}{n-1}$$個です。

この中でCardinal Treeのビット表現になっているものがどれくらいあるかを考えます。実は、これに関して次の2つの事実が成り立ちます。

1. 長さnkで1をn-1個含むビット列を長さkの区間に分割し、分割してできたn個の区間に先頭から番号を1,2,..,nとつけていく。この区間列1,2,...,nを、1以上n以下の整数iに対してi,i+1,...,n,1,2,...,i-1と並べ替える操作を回転とよぶことにする。このとき、区間列1,2,...,nを回転させてできるn通りのビット列はすべて異なる。
2. 長さnkで1をn-1個含むビット列に対して、回転させてできるn通りを考えると、その中でただ一つだけCardinal Treeのビット表現になっている。

この2つの事実が証明できたとすると、長さnkで1をn-1個含むビット列の中で、Cardinal Treeのビット表現となっているものは$$\frac{\binom{nk}{n-1}}{n}=\frac{\binom{nk+1}{n}}{nk+1}$$個であることがわかるので、頂点数nのCardinal Treeの個数は$$\frac{\binom{nk+1}{n}}{nk+1}$$個であるとわかります。

ではこの2つの事実を証明してみましょう。

1.の証明

 長さnkで1をn-1個含むビット列を、長さkの区間ごとに分割して区間に番号をつけて並べたものを1,2,...,nとする。これを回転させてできるn通りの中に同じビット列があるとき、区間列は周期性を持つはずである。区間j個で1周期をなしているとすると、jは区間数nの約数である。ここで、1周期の中で含まれる1の個数をc個とすると、ビット列全体に含まれる1の個数はcn/j個である。これはn-1に等しいが、nとn-1は互いに素なのでj=nである必要がある。つまり区間n個で1周期なので、区間列は周期性を持たず、区間列を回転させてできるn通りのビット列はすべて異なる。

2.の証明

 1.の証明と同様のビット列、区間分割を考える。ここで、各区間に対して、区間に入っている1の数-1を返す関数$f(i)$($i$は区間番号)を考える。さらに、$f(1)$から$f(i)$までの累積和を$g(i)(1\leq i\leq n)$と表すことにする。このとき、前にCardinal Treeのビット表現の例で出てきたビット列に対する$g(i)(1\leq i\leq 9)$をグラフで表すと下図のようになる。

ここで$g(i)$を観察しながら、ビット列がCardinal Treeのビット表現になっているための条件を考えてみよう。Cardinal Treeのビット表現では、$g(i)(1\leq i\leq n)$は、頂点1,2,...,iを用いてCardinal Treeの部分木を作ったときに、その木の頂点が追加で持つ予定の子の個数-1を表している。つまり、Cardinal Treeのビット表現では、$g(i)$は$i=n$の場合を除いて非負である。

さて、Cardinal Treeのビット表現の特徴づけがわかったところで、長さnk、1をn-1個含む任意のビット列に対して、それを回転して得られるn通りのうちただ一つだけがCardinal Treeのビット表現になっていることを示そう。

実は、長さnk、1をn-1個含む任意のビット列に対して、$g(i)(1\leq i\leq n)$が最小であるような区間のうち最も左の区間（番号が最小の区間）iを見つけ、区間i+1が先頭になるように回転すればCardinal Treeのビット表現になっている。また、それ以外の区間が先頭になるように回転すると、それはCardinal Treeのビット表現にはなっていない。

まずは実際に例で確認してみよう。次のCardinal Treeのビット表現になっていないビット列に対する$g(i)(1\leq i\leq 9)$を観察してみる。

 この場合$g(i)$が最小である区間のうち、最も左の区間は6なので、7を先頭に回転してみる。

このとき、確かに回転後のビット列は$g(i)$が$i<9$において非負なので、Cardinal Treeのビット表現になっている。

また、ほかの区間を先頭にして回転すると、$g(i)$が$i<9$のどこかで負になることが確認できるだろう。

これは、$g(i)$が最小である区間のうち、最も左の区間をiとして、区間i+1が先頭になるように回転すると、区間iが回転後に$g$が最小になる唯一の区間であり、また区間i+1以外が先頭になるように回転すると、区間iでの$g$の値が回転後に負になるからである。

*1:証明のもととなるアイデアは一緒に輪講を受けていた学科同期から教えてもらいました。