数理情報学専攻予想問題

院試勉強にもそろそろ飽きてきたので、気分転換に数理情報学専攻の専門数学の予想問題を作ってみました。計数工学科内では有名な（？）話題に関する問題ですが、ちょっとマニアックなので、暇な人は解いてみてください。難易度は難しめ（&分量多め）だと思います。

問題

無向グラフ$G=(V, E)$を、2つの頂点集合$R, C\subseteq V$（$R\cap C=\emptyset, R\cup C=V$）と、辺集合$E\subseteq \{(r, c)\mid r\in R, c\in C \}$をもつ2部グラフとする。この2部グラフ$G$に対して、DM分解（Dulmage-Mendelsohn分解）と呼ばれる頂点集合$V$の分割を考える。まず、DM分解は次のようなアルゴリズムによって得られる:

DM分解アルゴリズム

$G$の最大マッチング$M $を1つ見つけ、$M $の端点の集合を$\partial M $とする。
$G$において、$E\setminus M $の辺を$R$から$C$へ向かうように向き付けした有向辺と、$M $の辺を$R$から$C$、$C$から$R$へ向かうようにそれぞれ向き付けした有向辺からなる集合を$\tilde{E}$とする。$\tilde{G}=(V, \tilde{E})$とする。
$\tilde{G}$において、$R\setminus \partial M $の頂点から有向辺をたどって到達できる頂点全体の集合（$R\setminus \partial M $の頂点も含む）を$V_{\infty}$とし、$C\setminus \partial M $の頂点に有向辺をたどって到達できる頂点全体の集合を$V_{0}$とする。
$\tilde{G}$から$V_0\cup V_{\infty}$の頂点（とそれに接続する辺）を除去したグラフの強連結成分分解$\{V_k \mid 1\leq k \leq p\}(\emptyset \neq V_k \subseteq V)$を求める。ただし、$V_1, V_2, ..., V_p$は強連結成分であり、$l<k$のとき$V_k$から$V_l$への有向道がないように番号づける。

ここで得られた$V$の分割$\{V_k \mid k=0, 1, ...,p, \infty \}$のことを$G$のDM分解と呼ぶ。

(1) 次の図1の2部グラフ$H$のDM分解（頂点集合の分割）を求めよ。

f:id:mizuwater0:20190814235850p:plain

以下、$G$のDM分解$\{V_k \mid k=0, 1, ...,p, \infty \}$について考える。

(2) 頂点集合$(R\setminus V_{\infty})\cup (C\cap V_{\infty})$が$G$の最小頂点被覆であることを示せ。

(3) 頂点集合$V$において、頂点$s, t$を新たに追加し、$V'=V\cup \{s, t\}$とする。また、頂点$s$から$R$の各頂点へのコスト1の有向辺と、$C$の各頂点から$t$へのコスト1の有向辺、および$E$の各辺を$R$から$C$へ向かうように向き付けしたコスト2の有向辺からなる辺の集合を$E'$とする。$G'=(V', E')$とする。このとき、カット$(\{s\}\cup V_{\infty}, \ V'\setminus (\{s\}\cup V_{\infty}))$が$G'$の最小$s$-$t$カットであることを示せ。ただし、$G'$の最小$s$-$t$カットとは、頂点$s$と$t$を分離するカットのうち、コストが最小のカットのことである。

(4) $\{V_k \mid k=0,1,...,p, \infty\}$に対して次のように半順序を定める:

$V_k \preceq V_l \Longleftrightarrow k=\infty$または$l=0$または$\tilde{G}$において$V_l$の頂点から$V_k$の頂点への有向道が存在する

この半順序から定まるイデアル全体の族を$I$とする。つまり、

$I=\{A \mid A\subseteq \{V_k \mid k=0,...,p,\infty\},V_l \in A$かつ$V_k \preceq V_l $なら$V_k\in A \}$

このとき、$\forall A\in I(A\neq \emptyset, \{V_k \mid k=0,...,p,\infty\})$について、$S_A=\{v \mid v=s$ または$\exists V_k\in A,\ v\in V_k\}$とすると、カット$(S_A,V'\setminus S_A)$が$G'$の最小$s$-$t$カットであることを示せ。

(5) 逆に、$G'$の任意の最小$s$-$t$カットはある$A\in I$を用いて$(S_A,V'\setminus S_A)$と表せることを示せ。

解答↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓

解答（略解）

(1)

f:id:mizuwater0:20190815114202p:plain

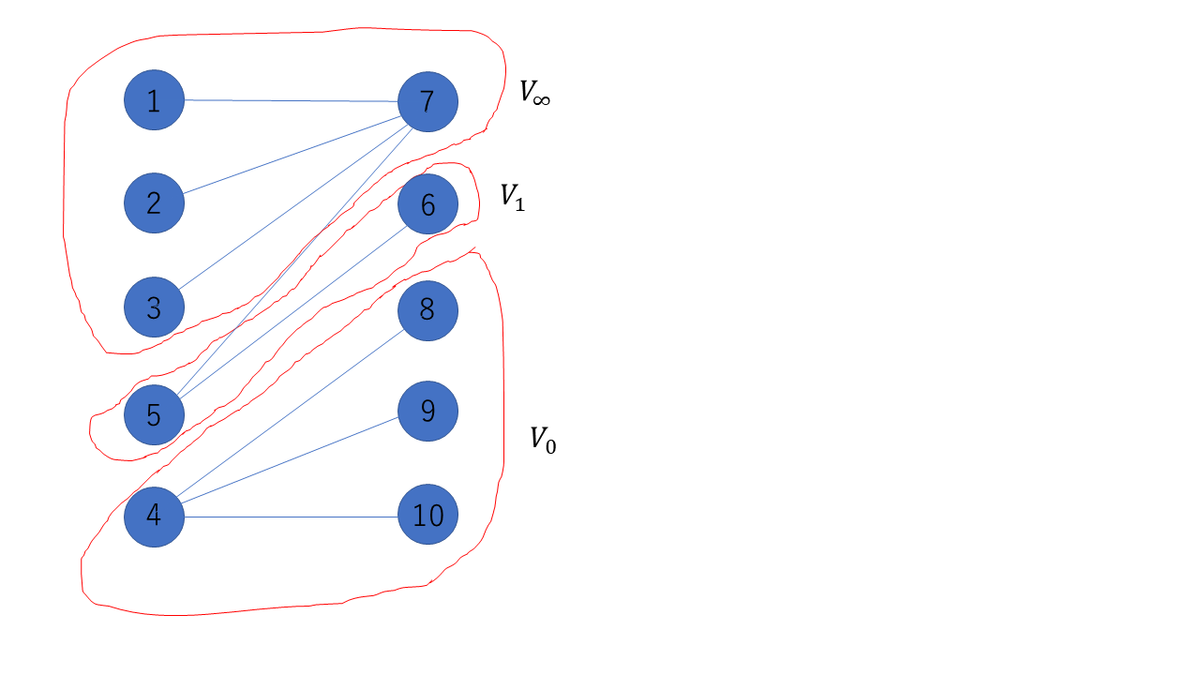
(2) $(R\setminus V_{\infty})\cup (C\cap V_{\infty})$が$G$の頂点被覆であることは構成からわかる。最小性は、被覆に必要な頂点数は最大マッチングの本数で下から抑えられるが、$(R\setminus V_{\infty})\cup (C\cap V_{\infty})$の頂点数は最大マッチング$M $の本数に等しいのでOK。

(3) 最大マッチング$M $の各辺$(r,c)(r\in R,\ c\in C)$について、$s\rightarrow r\rightarrow c\rightarrow t$という有向道に着目する。

f:id:mizuwater0:20190815120903j:plain

すると、この有向道の辺$(s, r), (r, c), (c, t)$のうち少なくとも1本は$s$と$t$を分離するカットに含まれることがわかる。ゆえに、最小$s$-$t$カットのコストは最大マッチング$M $の本数で下から抑えられるが、カット$(\{s\}\cup V_{\infty}, \ V'\setminus (\{s\}\cup V_{\infty}))$のコストは最大マッチング$M $の本数に等しいので、このカットは最小$s$-$t$カットである。

(4) カット$(S_A,V'\setminus S_A)$のコストは(3)の最小$s$-$t$カットとのコストと同じなので、$(S_A,V'\setminus S_A)$も最小$s$-$t$カット。

(5) $G'$において$s$から最大流を流して（コストを辺容量とみる、最大流は最大マッチング$M $に流れるようにする）残余グラフをとる。このとき残余グラフ上で容量をコストとみたときのコスト0の$s$-$t$カット全体は(4)で出てきたカット$(S_A, V'\setminus S_A)$全体に等しい。また、この残余グラフ上のコスト0の$s$-$t$カット全体は$G'$の最小$s$-$t$カット全体に等しい。よって、$G'$の$s$-$t$最小カット全体は、(4)で出てきたカット$(S_A,V'\setminus S_A)$全体に等しい（(3)と(4)も実はこれで示せます）。

解説

ここで問題の背景について少し解説します。

任意のグラフに対して最大流を流して残余グラフを構成し、そのグラフ上で始点（ソース）からたどりつける頂点全体の集合、終点（シンク）にたどりつける頂点全体の集合、それらを残余グラフから除いて強連結成分分解して得られた強連結成分をそれぞれとります。これに対して互いの頂点集合を行き来できるかという半順序を定義し、その半順序から定まるイデアル族をとると、実はこれが最小カット全体の集合になっている、という事実が成り立ちます。これの2部グラフでの特殊な場合がDM分解となるわけです。